Les LLMs sont-ils vraiment capables de raisonner ?

💡 Les LLMs sont-ils vraiment capables de raisonner ?

Les grands modèles de langage (LLM) ont révolutionné l’intelligence artificielle en démontrant des capacités impressionnantes pour comprendre et générer du langage naturel.

Cependant, une nouvelle étude d’Apple révèle une réalité troublante : ces modèles manquent cruellement de compétences en raisonnement formel.

🧠 Les LLMs et le raisonnement : un défaut structurel ?
Les scientifiques d’Apple et de l’Université de Californie ont constaté que les LLMs échouent à résoudre des problèmes de raisonnement, en particulier dans les contextes où le raisonnement déductif et contre-factuel est requis. Leur étude souligne qu’aucune preuve de raisonnement mathématique cohérent n’a été trouvée chez ces modèles. De plus, leur sensibilité à de légères modifications dans la formulation des requêtes (benchmark GSM-Symbolic) met en lumière leur fragilité face à des tâches de raisonnement.

📊 La preuve par les faits : GSM-Symbolic
Le benchmark GSM-Symbolic montre que de simples variations dans les valeurs numériques ou l’ajout d’informations contextuelles inutiles peuvent faire chuter la précision des réponses des LLMs jusqu’à 65 %, ce qui met en cause leur capacité à raisonner de manière fiable et nous rappelle que ces modèles sont davantage des appariements sophistiqués que des agents logiques.

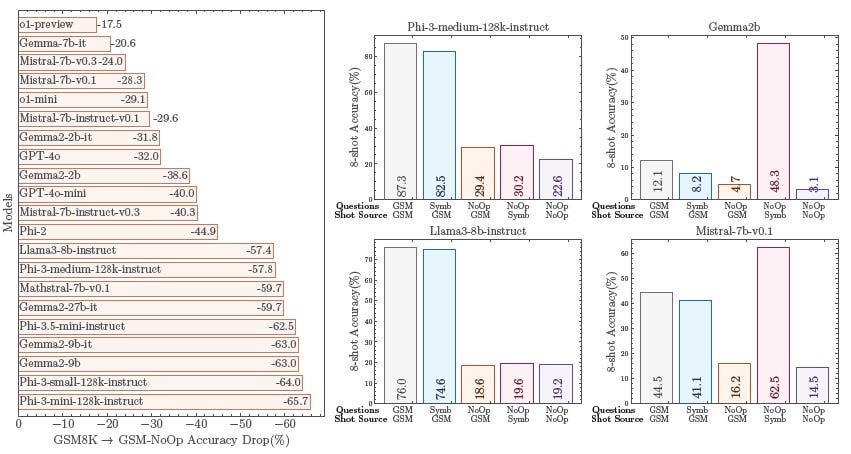
🤔 Pourquoi les LLMs échouent-ils dans les tâches complexes de raisonnement ?
Les LLMs sont conçus pour reconnaître des patterns dans d’énormes quantités de données, ce qui leur confère une aptitude impressionnante à générer des réponses basées sur des similitudes linguistiques. Cependant, ces modèles ne sont pas conçus pour effectuer des raisonnements formels. Ils échouent notamment dans les tâches requérant une pensée déductive, car ils n’ont pas été initialement conçus pour structurer leur logique de manière explicite.

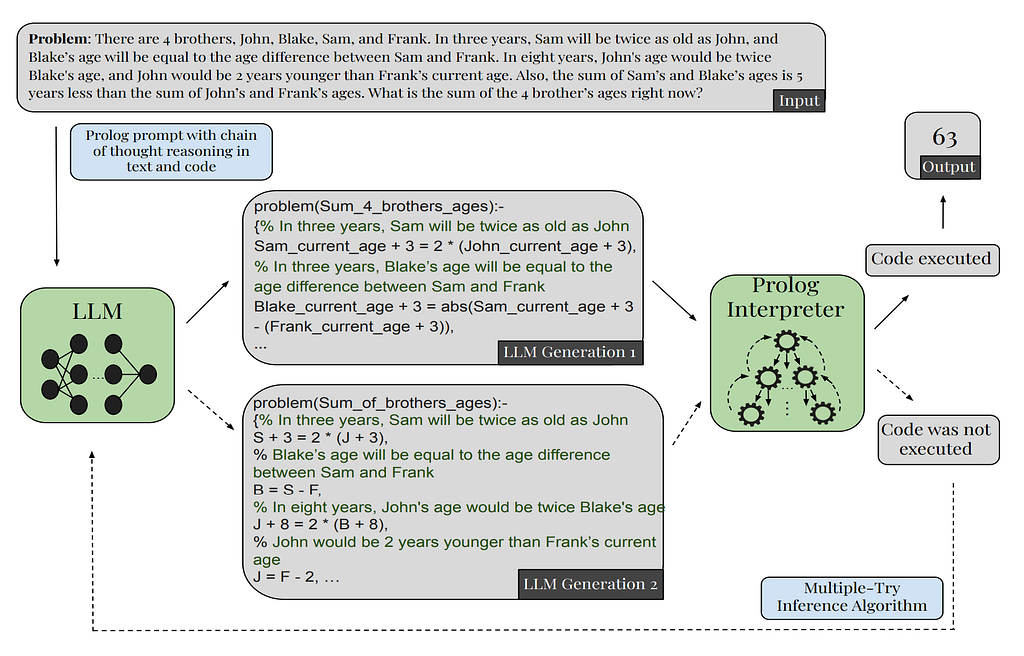
🤖 Comment Prolog peut-il sauver les LLMs ?
Les chercheurs commencent à explorer une approche neurosymbolique pour améliorer le raisonnement des LLMs.

Le langage Prolog, spécialisé dans le raisonnement basé sur des règles, devient un outil précieux pour combler les lacunes des modèles actuels. En convertissant des requêtes en code Prolog, les modèles peuvent générer des réponses plus robustes et fiables.

🌟 Prolog à la rescousse : l’exemple du Problème du Zèbre

Pour mieux comprendre pourquoi Prolog excelle dans le raisonnement, prenons un exemple pratique et complexe : le Problème du Zèbre. Ce problème de logique consiste à résoudre un logigramme où cinq personnes, habitant dans des maisons de couleurs différentes, avec chacune une nationalité, une boisson, une profession et un animal différents, doivent être placées en respectant certains indices, comme « l’Anglais habite la maison rouge » ou « la maison verte est juste à droite de la maison blanche ».

• Inspiré de Gecif.net

Pourquoi Prolog est-il adapté ?

Contrairement aux LLMs, qui tentent de répondre en fonction de modèles statistiques basés sur de grands corpus de texte, Prolog applique une logique pure et une structure de règles. Il n’essaie pas de “deviner” la réponse : il suit strictement les règles et les conditions fournies, garantissant ainsi une solution exacte lorsqu’elle existe.

🔧 Traduire le problème en Prolog : Exemple Simplifié

Pour illustrer, voici comment Prolog pourrait gérer ce problème :

1. Définir les maisons : On crée une liste de maisons, chacune ayant des attributs pour sa couleur, la nationalité de son occupant, son animal, sa boisson et sa profession.
2. Traduire les indices en règles : Chaque indice est converti en une condition que Prolog doit vérifier. Par exemple, « l’Anglais habite la maison rouge » devient une règle en Prolog pour associer la nationalité « Anglais » à la couleur « rouge ».

Voici une version simplifiée du code pour illustrer la logique :

% Définition de la liste des maisons
liste_des_maisons([
    maison(_, _, _, _, _),
    maison(_, _, _, _, _),
    maison(_, _, _, _, _),
    maison(_, _, _, _, _),
    maison(_, _, _, _, _)
]).

% Traduction des indices en règles Prolog
appartient_a(maison(rouge, anglais, _, _, _), MAISONS). 
% L'anglais habite la maison rouge
appartient_a(maison(_, espagnol, chien, _, _), MAISONS). 
% L'espagnol a un chien
est_a_droite_de(maison(verte, _, _, _, _), maison(blanche, _, _, _, _), MAISONS). % La maison verte est à droite de la maison blanche

🎯 Comment Prolog trouve-t-il la solution ?

En exécutant resoudre, Prolog parcourt toutes les règles et indices jusqu’à trouver une solution unique et cohérente. Contrairement aux LLMs qui pourraient interpréter un indice de manière approximative, Prolog garantit que chaque règle est respectée. Par exemple :

• Position des maisons : Prolog sait que « la maison verte est à droite de la blanche » et place donc obligatoirement ces deux maisons dans le bon ordre.
• Association des attributs : Chaque personne est correctement associée à une maison, un animal, une boisson, et ainsi de suite, selon les règles définies.

Résultat : Une fois toutes les règles appliquées, Prolog déduit que :

• Le Norvégien boit de l’eau.
• Le Japonais possède le zèbre.

🚀 Pourquoi Prolog raisonne mieux ?

1. Respect des règles sans approximation : Prolog ne s’éloigne jamais des règles. Chaque condition doit être vérifiée et respectée pour que le programme aboutisse, ce qui élimine les erreurs de raisonnement dues à des interprétations statistiques floues.

2. Ordre et structure : Prolog gère parfaitement les contraintes d’ordre (comme « est à droite de ») et les relations logiques complexes entre différents éléments, ce qui est crucial dans des logigrammes comme celui du Zèbre.

3. Pas de place pour l’ambiguïté : Les LLMs peuvent proposer des réponses différentes selon les formulations, mais Prolog garantit une solution unique ou signale s’il n’y en a aucune, assurant ainsi une réponse fiable et cohérente.

🔧 Pourquoi Prolog n’est-il pas intégré dès le départ ?
L’intégration de Prolog dans les LLMs représente un défi technique, car ces modèles ont été développés pour fonctionner en mode de reconnaissance de formes, tandis que Prolog repose sur des règles explicites de raisonnement.

Cette fusion entre deux paradigmes différents demande une ingénierie complexe, mais les premiers résultats montrent que cela pourrait résoudre des problèmes que les LLMs seuls ne parviennent pas à traiter.

📈 Un exemple frappant : GPT-4 et Prolog
Sur des tests complexes comme le Non-Linear Reasoning (NLR), GPT-4 combiné avec Prolog a réussi à résoudre 100 % des problèmes mathématiques posés, contre seulement 12,5 % avec une simple approche LLM + CoT.

Prolog permet non seulement d’améliorer les résultats, mais offre aussi une meilleure explicabilité des réponses.

🚀 La voie à suivre pour améliorer le raisonnement des LLMs
Les avancées avec Prolog montrent qu’il est possible d’améliorer la capacité des LLMs à raisonner en ajoutant des couches de raisonnement formel à leur architecture. Cette approche pourrait trouver des applications concrètes dans des domaines où la fiabilité et la précision des décisions sont cruciales, comme les systèmes critiques et l’IA industrielle. Les recherches futures devront se concentrer sur la création de modèles d’IA capables de passer de la simple reconnaissance de formes à un raisonnement plus robuste, fiable et général.

Sources:

• Shchegrikovich, A. (2024). Use Prolog to improve LLMs reasoning. Substack
• Développez.com (2024). L’étude d’Apple prouve que les modèles d’IA basés sur le LLM sont défectueux car ils ne peuvent pas raisonner.
• Résolution de problèmes avec Prolog — Gecif.net

#IntelligenceArtificielle #IA #OpenSource #LLM #Prolog #Apple #DeepLearning #NLP #Neurosymbolique #ChainOfThought #RaisonnementAI #ExplorationsTechniques #GPT4

💡 Les LLMs sont-ils vraiment capables de raisonner ? was originally published in P2Enjoy SAS (IA & Web3) on Medium, where people are continuing the conversation by highlighting and responding to this story.